
Conjoint Analysis- D-Optimal Design
Optimal designs are a class of experimental designs that are optimal with respect to some statistical criterion. In the design of experiments for estimating statistical models, optimal designs allow parameters to be estimated without bias and with minimum-variance. A non-optimal design requires a greater number of experimental runs to estimate the parameters with the same precision as an optimal design. In practical terms, optimal experiments can reduce the costs of experimentation.
Conjoint Analysis D-Optimal Design is a design based on D-Optimality for the Conjoint Analysis (Discrete Choice) question. In general, D-Optimality is a concept that uses a desired set of experiments to optimize or investigate a studied object. It seeks to minimize |(X'X)−1|, or equivalently maximize the determinant of the information matrix X'X of the design.
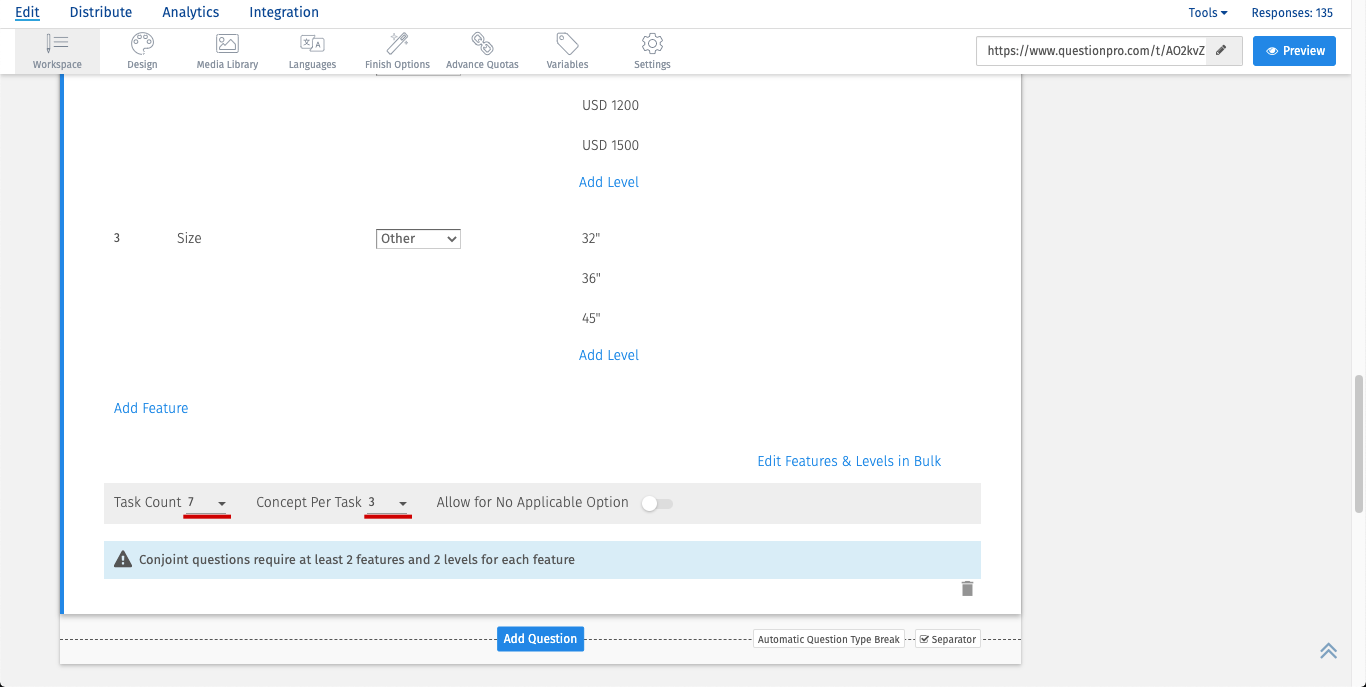
- Product of Task Count and Concept per task should be greater than or equal to:7
- Go to: Edit Conjoint Question >> Design Type
- Select Design Type as D-Optimal.
- Select versions.
- Click on Start.
- Click on Save Settings.
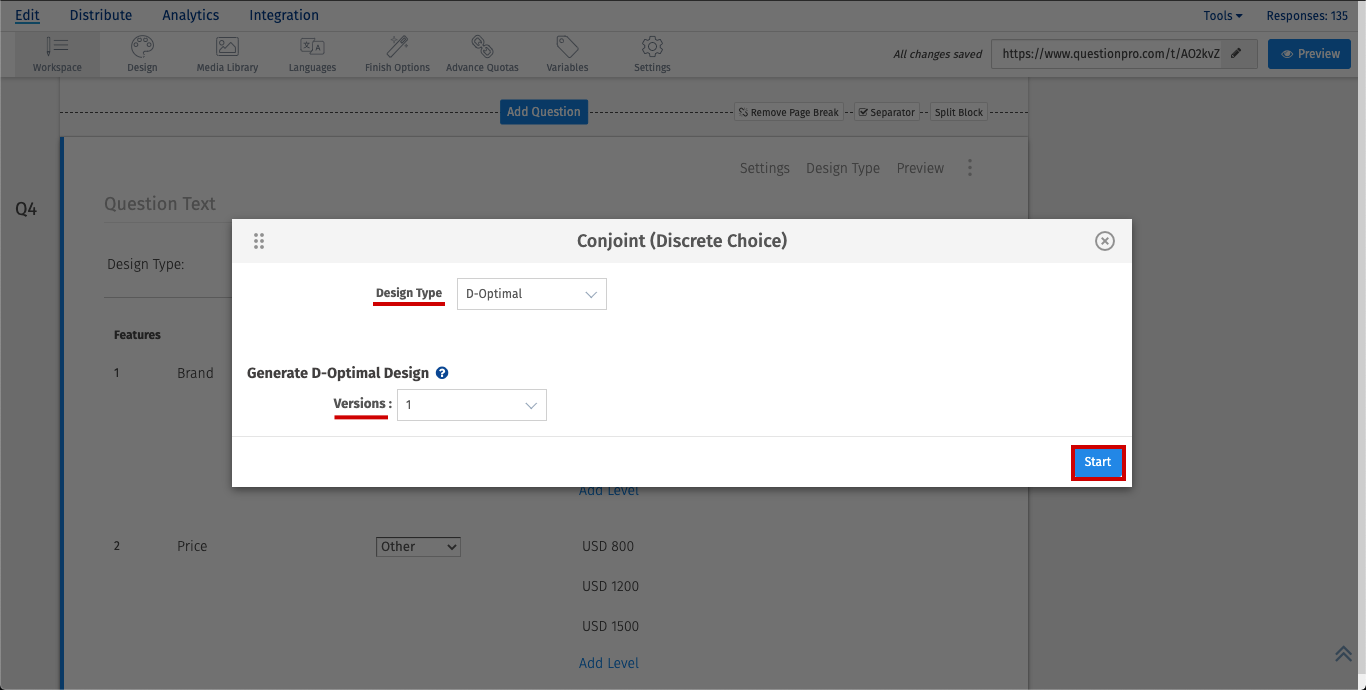
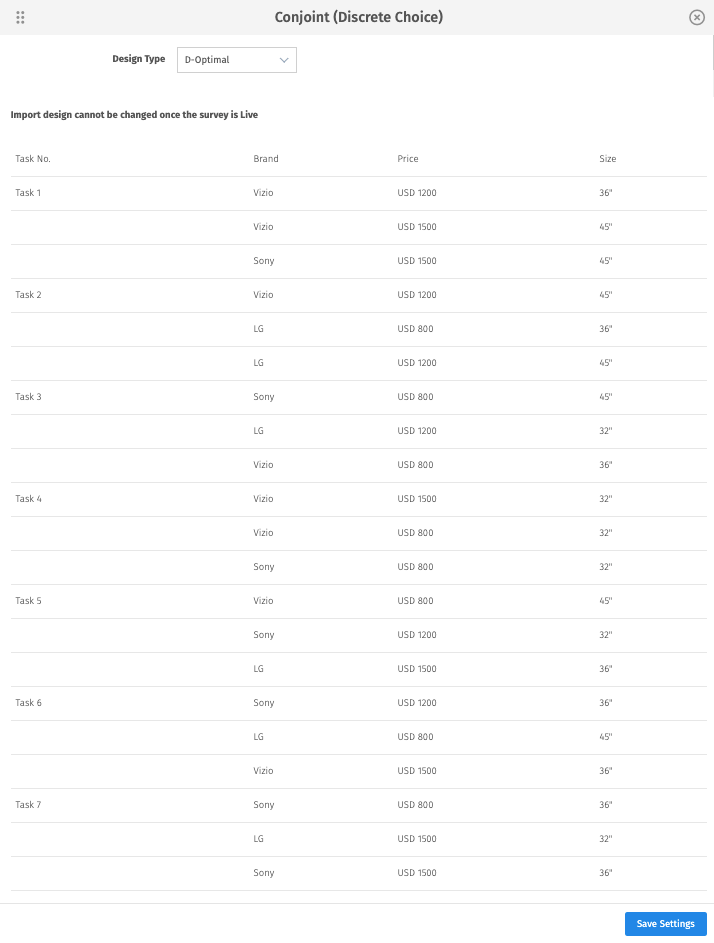
Here specify how many versions of the D-Optimal design would you like to generate. If multiple versions are selected, a large D-optimal design with total tasks equal to (the number of tasks specified) X ( the number of versions specified) will be generated. While taking survey each respondent will get as many tasks as specified in the question but these will be randomly chosen from large D-optimal design generated earlier.

